Analysis of xx-ph-00258027-12_12_03-base.sdk
Contents
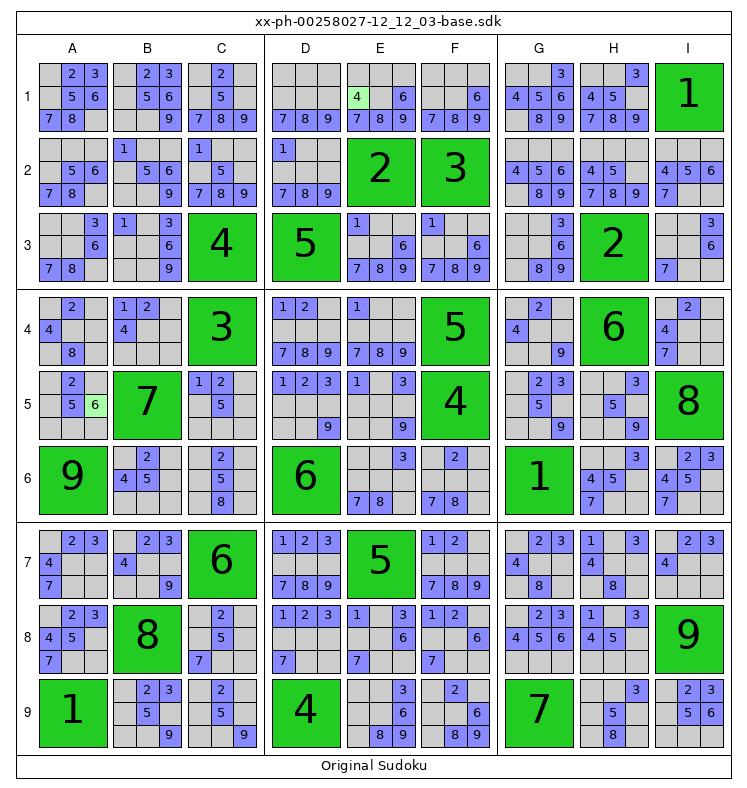
Original Sudoku
level: deep
position: ........1....23.....45...2...3..5.6..7...4..89..6..1....6.5.....8......91..4..7.. initial
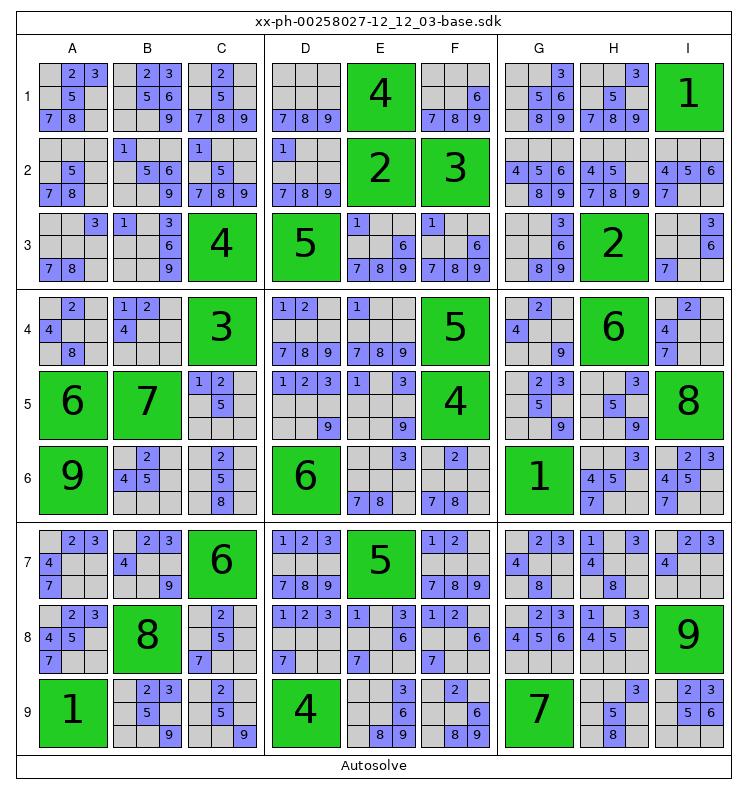
Autosolve
position: ....4...1....23.....45...2...3..5.6.67...4..89..6..1....6.5.....8......91..4..7.. autosolve
Pair Reduction Variants
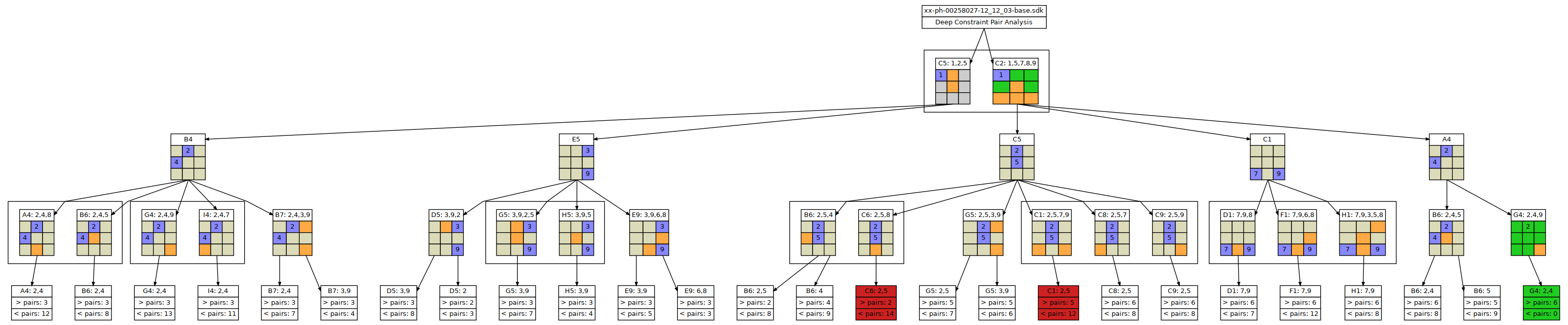
Deep Constraint Pair Analysis
Time used: 0:00:00.000007
List of important HDP chains detected for A4,C6: 8..:
* DIS # A4: 8 # C2: 5,7 => CTR => C2: 1,8,9 * DIS # A4: 8 + C2: 1,8,9 # A1: 3,7 => CTR => A1: 2,5 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 # C5: 2,5 => CTR => C5: 1 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 # C1: 2,5 => CTR => C1: 7,8,9 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 # C8: 2,5 => CTR => C8: 7 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 # B1: 3,6 => CTR => B1: 2,5 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 # F1: 8,9 => CTR => F1: 6,7 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 # G1: 8,9 => CTR => G1: 3,6 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 # H1: 8,9 => CTR => H1: 3,7 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 # G2: 8,9 => CTR => G2: 4,5 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 + G2: 4,5 # B6: 5 => CTR => B6: 2,4 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 + G2: 4,5 + B6: 2,4 # G4: 2,4 => CTR => G4: 9 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 + G2: 4,5 + B6: 2,4 + G4: 9 => CTR => A4: 2,4 * STA A4: 2,4 * CNT 13 HDP CHAINS / 40 HYP OPENED
List of important HDP chains detected for C2,C5: 1..:
* DIS # C2: 1 # C6: 2,5 => CTR => C6: 8 * DIS # C2: 1 + C6: 8 # C1: 2,5 => CTR => C1: 7,9 * PRF # C2: 1 + C6: 8 + C1: 7,9 # G4: 2,4 => SOL * STA # C2: 1 + C6: 8 + C1: 7,9 + G4: 2,4 * CNT 3 HDP CHAINS / 35 HYP OPENED
See Appendix: Full HDP Chains for full list of HDP chains.
Details
This sudoku is deep. Here is some information that may be helpful on how to proceed.
Positions
| ........1....23.....45...2...3..5.6..7...4..89..6..1....6.5.....8......91..4..7.. | initial |
| ....4...1....23.....45...2...3..5.6.67...4..89..6..1....6.5.....8......91..4..7.. | autosolve |
Classification
level: deep
Pairing Analysis
-------------------------------------------------- * CONSTRAINT PAIRS (AUTO SOLVE) B4,C5: 1.. / B4 = 1 => 1 pairs (_) / C5 = 1 => 2 pairs (_) H7,H8: 1.. / H7 = 1 => 0 pairs (_) / H8 = 1 => 0 pairs (_) C2,C5: 1.. / C2 = 1 => 1 pairs (_) / C5 = 1 => 2 pairs (_) G8,I9: 6.. / G8 = 6 => 0 pairs (_) / I9 = 6 => 1 pairs (_) A4,C6: 8.. / A4 = 8 => 3 pairs (_) / C6 = 8 => 3 pairs (_) * DURATION: 0:00:03.274021 START: 02:33:28.047247 END: 02:33:31.321268 2020-12-24 * CP COUNT: (5) * INCONCLUSIVE -------------------------------------------------- * DEEP CONSTRAINT PAIRS (PAIR REDUCTION) A4,C6: 8.. / A4 = 8 ==> 0 pairs (X) / C6 = 8 => 3 pairs (_) C2,C5: 1.. / C2 = 1 ==> 0 pairs (*) / C5 = 1 ==> 2 pairs (_) * DURATION: 0:00:43.318890 START: 02:33:31.321865 END: 02:34:14.640755 2020-12-24 * REASONING A4,C6: 8.. * DIS # A4: 8 # C2: 5,7 => CTR => C2: 1,8,9 * DIS # A4: 8 + C2: 1,8,9 # A1: 3,7 => CTR => A1: 2,5 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 # C5: 2,5 => CTR => C5: 1 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 # C1: 2,5 => CTR => C1: 7,8,9 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 # C8: 2,5 => CTR => C8: 7 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 # B1: 3,6 => CTR => B1: 2,5 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 # F1: 8,9 => CTR => F1: 6,7 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 # G1: 8,9 => CTR => G1: 3,6 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 # H1: 8,9 => CTR => H1: 3,7 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 # G2: 8,9 => CTR => G2: 4,5 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 + G2: 4,5 # B6: 5 => CTR => B6: 2,4 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 + G2: 4,5 + B6: 2,4 # G4: 2,4 => CTR => G4: 9 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 + G2: 4,5 + B6: 2,4 + G4: 9 => CTR => A4: 2,4 * STA A4: 2,4 * CNT 13 HDP CHAINS / 40 HYP OPENED * REASONING C2,C5: 1.. * DIS # C2: 1 # C6: 2,5 => CTR => C6: 8 * DIS # C2: 1 + C6: 8 # C1: 2,5 => CTR => C1: 7,9 * PRF # C2: 1 + C6: 8 + C1: 7,9 # G4: 2,4 => SOL * STA # C2: 1 + C6: 8 + C1: 7,9 + G4: 2,4 * CNT 3 HDP CHAINS / 35 HYP OPENED * DCP COUNT: (2) * SOLUTION FOUND
Header Info
258027;12_12_03;dob;22;11.30;1.20;1.20
Appendix: Full HDP Chains
A1. Deep Constraint Pair Analysis
Full list of HDP chains traversed for A4,C6: 8..:
* INC # A4: 8 # A1: 5,7 => UNS * INC # A4: 8 # C1: 5,7 => UNS * DIS # A4: 8 # C2: 5,7 => CTR => C2: 1,8,9 * INC # A4: 8 + C2: 1,8,9 # H2: 5,7 => UNS * INC # A4: 8 + C2: 1,8,9 # I2: 5,7 => UNS * INC # A4: 8 + C2: 1,8,9 # A8: 5,7 => UNS * INC # A4: 8 + C2: 1,8,9 # A8: 2,3,4 => UNS * INC # A4: 8 + C2: 1,8,9 # A1: 5,7 => UNS * INC # A4: 8 + C2: 1,8,9 # C1: 5,7 => UNS * INC # A4: 8 + C2: 1,8,9 # H2: 5,7 => UNS * INC # A4: 8 + C2: 1,8,9 # I2: 5,7 => UNS * INC # A4: 8 + C2: 1,8,9 # A8: 5,7 => UNS * INC # A4: 8 + C2: 1,8,9 # A8: 2,3,4 => UNS * DIS # A4: 8 + C2: 1,8,9 # A1: 3,7 => CTR => A1: 2,5 * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 # I3: 3,7 => UNS * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 # I3: 6 => UNS * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 # A7: 3,7 => UNS * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 # A8: 3,7 => UNS * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 # C5: 2,5 => CTR => C5: 1 * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 # B6: 2,5 => UNS * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 # B6: 2,5 => UNS * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 # B6: 4 => UNS * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 # C1: 2,5 => CTR => C1: 7,8,9 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 # C8: 2,5 => CTR => C8: 7 * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 # B6: 2,5 => UNS * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 # B6: 4 => UNS * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 # B1: 2,5 => UNS * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 # B1: 3,6 => CTR => B1: 2,5 * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 # A8: 2,5 => UNS * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 # A8: 4 => UNS * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 # D1: 8,9 => UNS * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 # F1: 8,9 => CTR => F1: 6,7 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 # G1: 8,9 => CTR => G1: 3,6 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 # H1: 8,9 => CTR => H1: 3,7 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 # G2: 8,9 => CTR => G2: 4,5 * INC # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 + G2: 4,5 # B6: 2,4 => UNS * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 + G2: 4,5 # B6: 5 => CTR => B6: 2,4 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 + G2: 4,5 + B6: 2,4 # G4: 2,4 => CTR => G4: 9 * DIS # A4: 8 + C2: 1,8,9 + A1: 2,5 + C5: 1 + C1: 7,8,9 + C8: 7 + B1: 2,5 + F1: 6,7 + G1: 3,6 + H1: 3,7 + G2: 4,5 + B6: 2,4 + G4: 9 => CTR => A4: 2,4 * INC A4: 2,4 # C6: 8 => UNS * STA A4: 2,4 * CNT 40 HDP CHAINS / 40 HYP OPENED
Full list of HDP chains traversed for C2,C5: 1..:
* INC # C5: 1 # A4: 2,4 => UNS * INC # C5: 1 # B6: 2,4 => UNS * INC # C5: 1 # G4: 2,4 => UNS * INC # C5: 1 # I4: 2,4 => UNS * INC # C5: 1 # B7: 2,4 => UNS * INC # C5: 1 # B7: 3,9 => UNS * INC # C5: 1 # D5: 3,9 => UNS * INC # C5: 1 # D5: 2 => UNS * INC # C5: 1 # G5: 3,9 => UNS * INC # C5: 1 # H5: 3,9 => UNS * INC # C5: 1 # E9: 3,9 => UNS * INC # C5: 1 # E9: 6,8 => UNS * INC # C5: 1 => UNS * INC # C2: 1 # B6: 2,5 => UNS * DIS # C2: 1 # C6: 2,5 => CTR => C6: 8 * INC # C2: 1 + C6: 8 # B6: 2,5 => UNS * INC # C2: 1 + C6: 8 # B6: 4 => UNS * INC # C2: 1 + C6: 8 # G5: 2,5 => UNS * INC # C2: 1 + C6: 8 # G5: 3,9 => UNS * DIS # C2: 1 + C6: 8 # C1: 2,5 => CTR => C1: 7,9 * INC # C2: 1 + C6: 8 + C1: 7,9 # C8: 2,5 => UNS * INC # C2: 1 + C6: 8 + C1: 7,9 # C9: 2,5 => UNS * INC # C2: 1 + C6: 8 + C1: 7,9 # B6: 2,5 => UNS * INC # C2: 1 + C6: 8 + C1: 7,9 # B6: 4 => UNS * INC # C2: 1 + C6: 8 + C1: 7,9 # G5: 2,5 => UNS * INC # C2: 1 + C6: 8 + C1: 7,9 # G5: 3,9 => UNS * INC # C2: 1 + C6: 8 + C1: 7,9 # C8: 2,5 => UNS * INC # C2: 1 + C6: 8 + C1: 7,9 # C9: 2,5 => UNS * INC # C2: 1 + C6: 8 + C1: 7,9 # D1: 7,9 => UNS * INC # C2: 1 + C6: 8 + C1: 7,9 # F1: 7,9 => UNS * INC # C2: 1 + C6: 8 + C1: 7,9 # H1: 7,9 => UNS * INC # C2: 1 + C6: 8 + C1: 7,9 # B6: 2,4 => UNS * INC # C2: 1 + C6: 8 + C1: 7,9 # B6: 5 => UNS * PRF # C2: 1 + C6: 8 + C1: 7,9 # G4: 2,4 => SOL * STA # C2: 1 + C6: 8 + C1: 7,9 + G4: 2,4 * CNT 34 HDP CHAINS / 35 HYP OPENED