Variables, Truth Table, Resolution and Expansion
| Author: | Wolfgang Scherer |
|---|
Contents
Variables
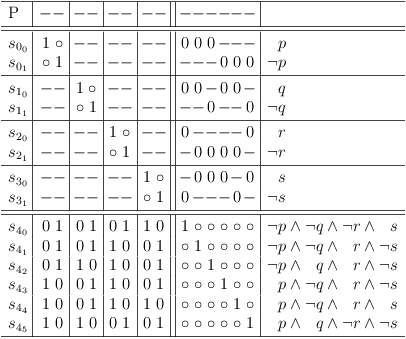
In the context of a satoku matrix, boolean variables appear as clause sub-matrixes with 2 selection rows, where one selection row represents the unnegated variable and the other selection row represents the negated variable. The clause sub-matrix of a variable therefore represents the clause (p∨¬p) .

Representation of variables in a satoku matrix
Since a clause sub-matrix represents possible selections and their dependencies, the variable representation is consistent with the axioms of logic.
- A variable can be true or false (p = T)∨(p = F), p∨¬p = T . Selection s00 is interpreted as p = T , selection s01 is interpreted as p = F . Both selections are possible, therefore (p = T)∨(p = F) .
- A variable cannot be both true and false p∧¬p = F . The dependency s00, 01 (and its mirror s01, 00 ) does not allow selecting both a variable and its negation.
Truth Table
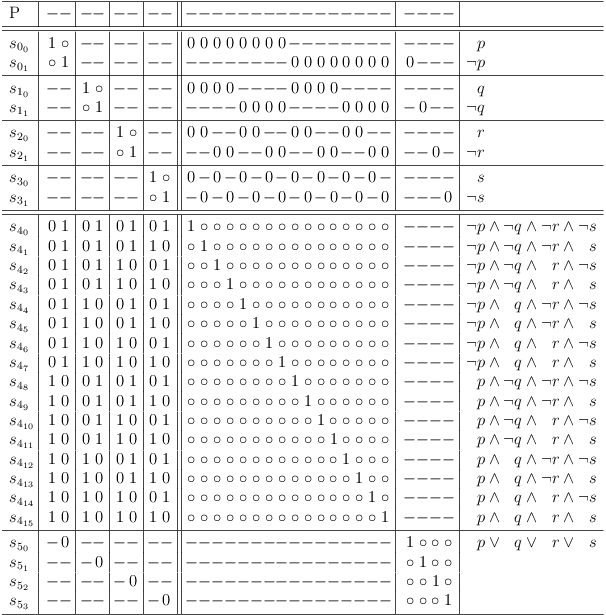
An unrestricted truth table for n variables appears as a clause sub-matrix with 2n selection rows. Each selection row represents one of the possible conjunctions of the variables.
Unrestricted Truth Table for 4 Variables
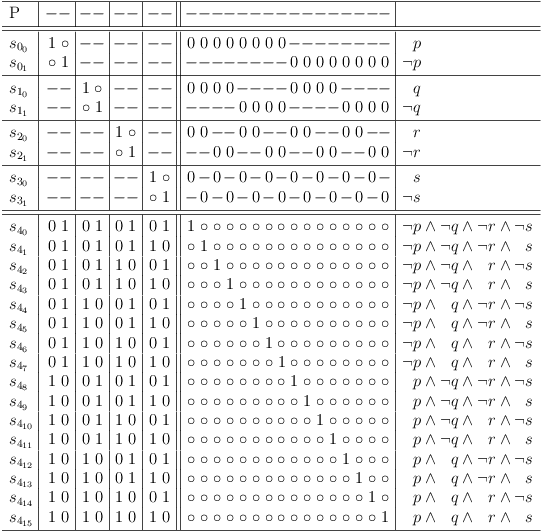
Unrestricted Truth Table for 4 Variables
The unrestricted truth table for 4 variables can therefore be interpreted as representation of a disjunction of all possible conjunctions for 4 variables:
( ( ¬p ∧ ¬q ∧ ¬r ∧ ¬s ) ∨ ( ¬p ∧ ¬q ∧ ¬r ∧ s ) ∨ ( ¬p ∧ ¬q ∧ r ∧ ¬s ) ∨ ( ¬p ∧ ¬q ∧ r ∧ s ) ∨ ( ¬p ∧ q ∧ ¬r ∧ ¬s ) ∨ ( ¬p ∧ q ∧ ¬r ∧ s ) ∨ ( ¬p ∧ q ∧ r ∧ ¬s ) ∨ ( ¬p ∧ q ∧ r ∧ s ) ∨ ( p ∧ ¬q ∧ ¬r ∧ ¬s ) ∨ ( p ∧ ¬q ∧ ¬r ∧ s ) ∨ ( p ∧ ¬q ∧ r ∧ ¬s ) ∨ ( p ∧ ¬q ∧ r ∧ s ) ∨ ( p ∧ q ∧ ¬r ∧ ¬s ) ∨ ( p ∧ q ∧ ¬r ∧ s ) ∨ ( p ∧ q ∧ r ∧ ¬s ) ∨ ( p ∧ q ∧ r ∧ s ) )
Mapping Logical Functions from a Truth Table
The following examples for mapping a disjunction and a conjunction of 4 variables as well as an arbitrarily defined function F, are used to illustrate the mapping options.
| p | q | r | s | p ∨ q ∨ r ∨ s | p ∧ q ∧ r ∧ s | F |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 |
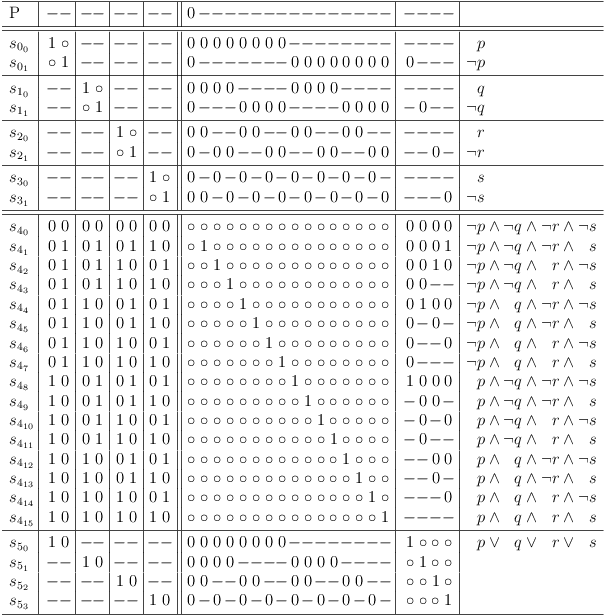
Disable Selection in Unrestricted Truth Table
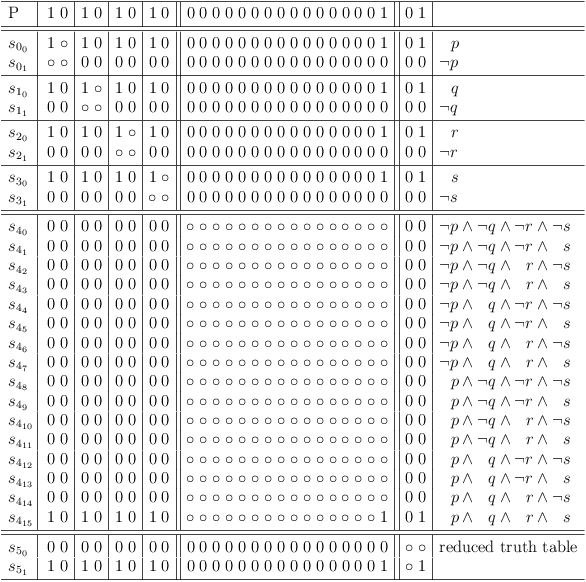
If the result of a logical function in a truth table row is 0, the corresponding selection in the unrestricted truth table clause of the satoku matrix is made impossible. I.e., the entire selection row is filled with zeroes.
Map disjunction of 4 variables
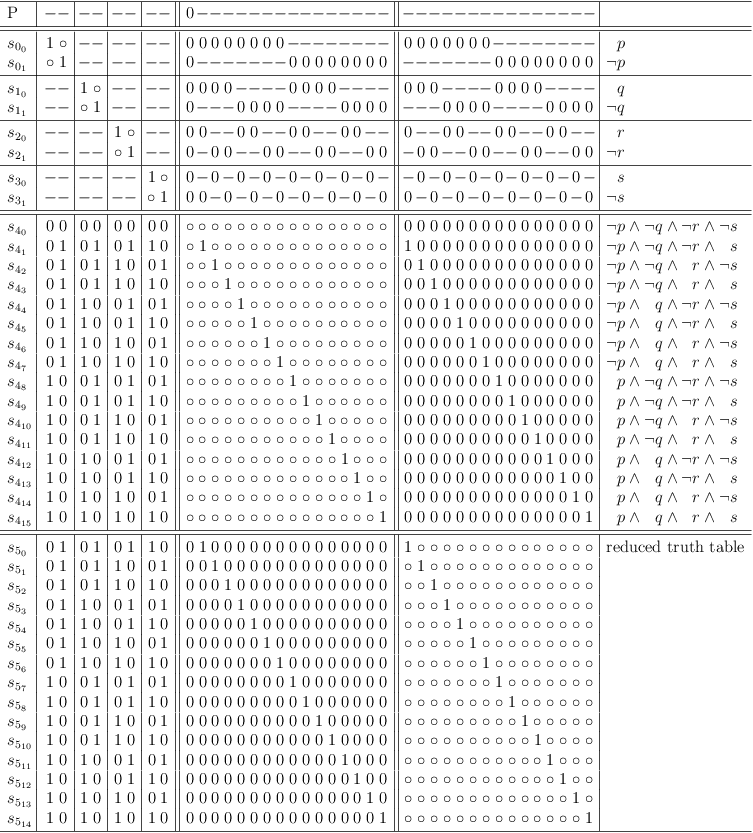
Map disjunction of 4 variables
Map conjunction of 4 variables
Map conjunction of 4 variables
Map arbitrary function F over 4 variables
Map arbitrary function F over 4 variables
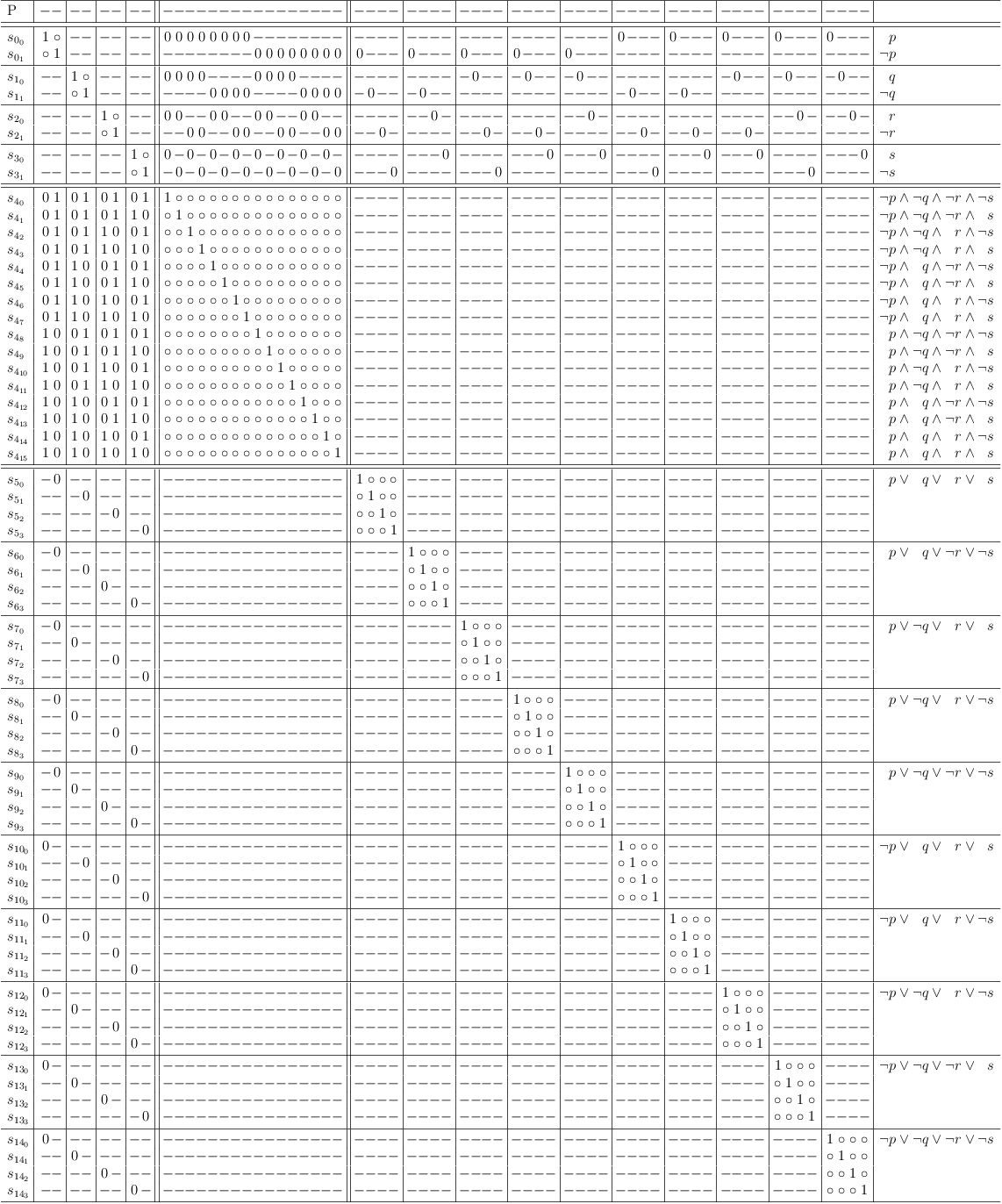
Construct Possible Selections
Instead of disabling selection rows in an unrestricted truth table clause, it is sufficient to construct a clause with the possible selections directly.
For function F, the clause is:
( ( ¬p ∧ ¬q ∧ ¬r ∧ s ) ∨ ( ¬p ∧ ¬q ∧ r ∧ ¬s ) ∨ ( ¬p ∧ q ∧ r ∧ ¬s ) ∨ ( p ∧ ¬q ∧ r ∧ ¬s ) ∨ ( p ∧ ¬q ∧ r ∧ s ) ∨ ( p ∧ q ∧ ¬r ∧ ¬s ) )
which maps to:
Map arbitrary function F over 4 variables directly
Add Constraints for Invalid Selections
The rows with a result of 0 can also be added as clauses. The corresponding conjunction of variables is negated and added as disjunctive clause.
For the disjunction example, the constraint is:
( ¬p ∧ ¬q ∧ ¬r ∧ ¬s ) = F
which is negated:
¬( ¬p ∧ ¬q ∧ ¬r ∧ ¬s ) = T
and converted to a disjunctive clause:
( p ∨ q ∨ r ∨ s ) = T
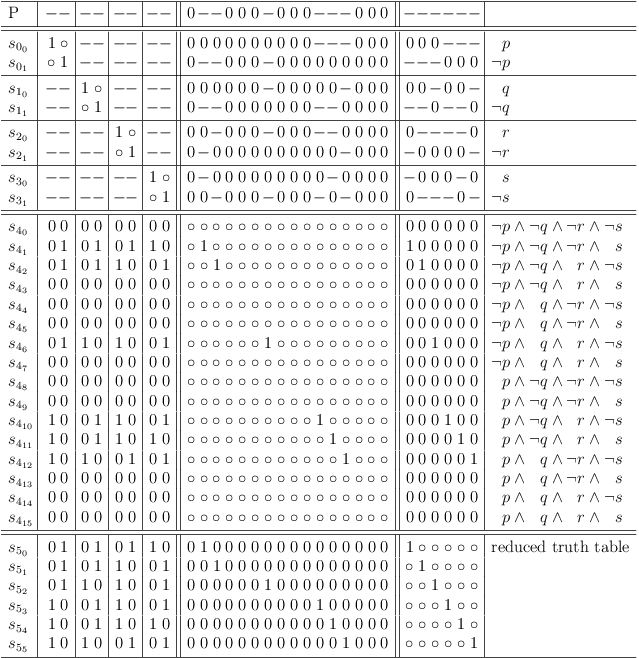
Map the constraint clause into the satoku matrix by adding requests for the variables of the disjunctive clause:
Add constraint requests for disjunction
Updating requirements for the disjunctive constraint, disables selection row s40 :
Updating requirements for disjunctive constraint disables s40
The constraints for function F are:
( p ∨ q ∨ r ∨ s ) ∧ ( p ∨ q ∨ ¬r ∨ ¬s ) ∧ ( p ∨ ¬q ∨ r ∨ s ) ∧ ( p ∨ ¬q ∨ r ∨ ¬s ) ∧ ( p ∨ ¬q ∨ ¬r ∨ ¬s ) ∧ ( ¬p ∨ q ∨ r ∨ s ) ∧ ( ¬p ∨ q ∨ r ∨ ¬s ) ∧ ( ¬p ∨ ¬q ∨ r ∨ ¬s ) ∧ ( ¬p ∨ ¬q ∨ ¬r ∨ s ) ∧ ( ¬p ∨ ¬q ∨ ¬r ∨ ¬s )
Add constraint requests for function F
Add constraint requests for function F
Updating requirements for disjunctive constraints of function F disables selections in unrestricted truth table

Updating requirements for disjunctive constraints of function F disables selections in unrestricted truth table
Mapping Constraints Directly
As with the clause of possible selections, the constraint clauses can be mapped directly without the unrestricted truth table. This is equivalent to mapping a CNF problem to a satoku matrix:
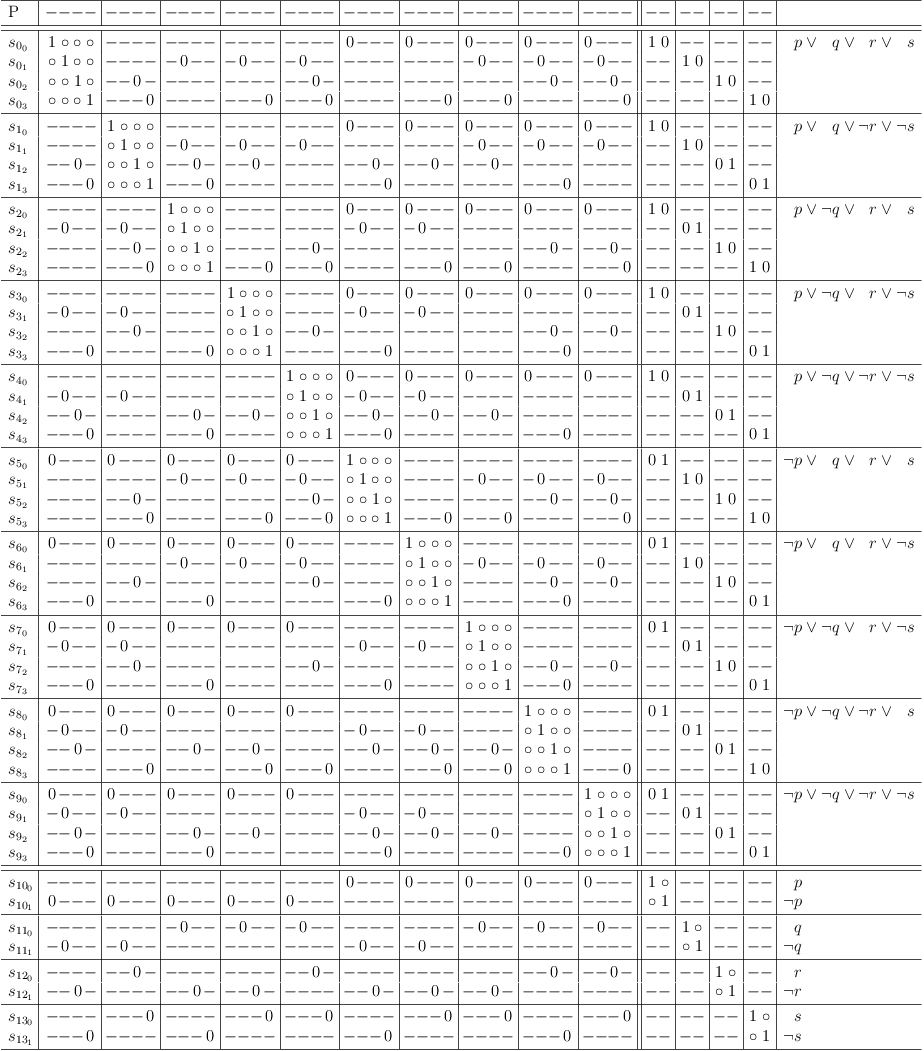
Map contraints of function F directly
Mapping the contraints of function F with conflict maximization, delivers the satoku matrix:

Map contraints of function F with conflict maximization
After removing impossible selections and redundancies, the satoku matrix presents as:
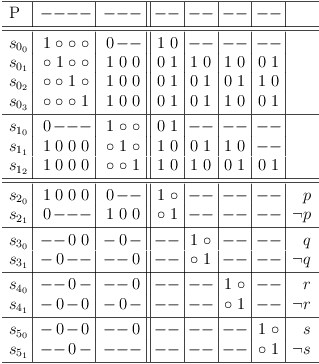
Contraints of function F cleaned up
Distributive expansion shows, that the solution set is equivalent to the truth table clause for function F above:

Distributive expansion for constraints of function F
Resolution and Expansion
Disjunctive resolution is derived from:
(p ∧ q ∧ r) ∨ (p ∧ q ∧ ¬r) = ((p ∧ q ∧ r) ∨ p) ∧ ((p ∧ q ∧ r) ∨ q) ∧ ((p ∧ q ∧ r) ∨ ¬r) = p ∧ q ∧ (p ∨ ¬r) ∧ (q ∨ ¬r) ∧ (r ∨ ¬r) = p ∧ q
Disjunctive resolution is denoted here as sij∩sfg .
By applying pair-wise resolution consecutively to the truth table clause of a 4 variable disjunction S4 , clause sub-matrix S7 can be derived:
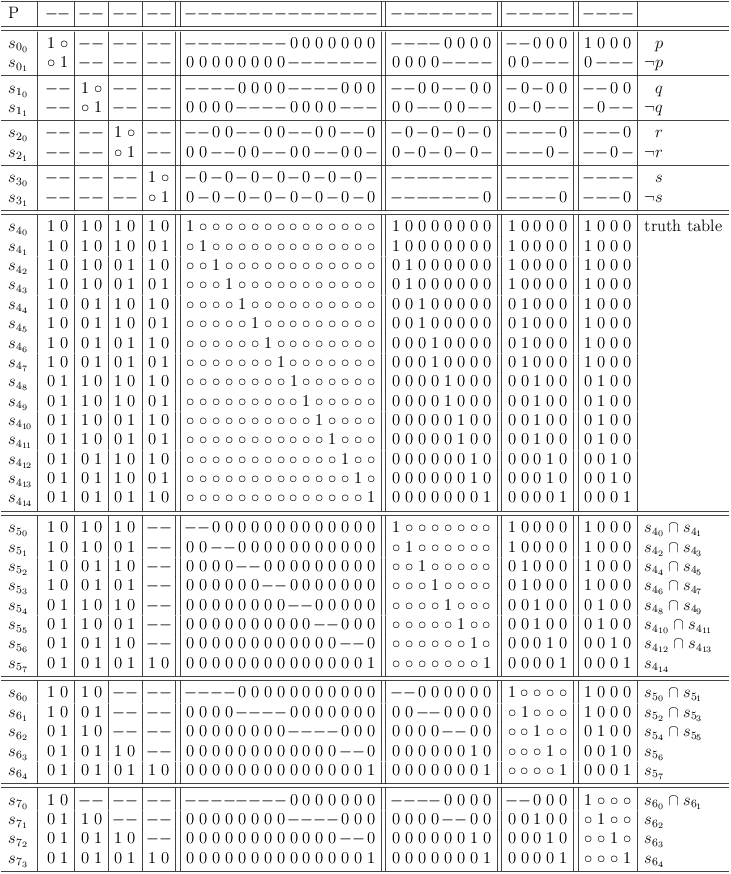
Continuous pair-wise resolution
Disjunctive expansion is based on:
(p ∧ q) ∨ (p ∧ q ∧ r) = (p ∧ q)
It is therefore allowed to add longer conjunctions to a disjunctive clause.
Applying disjunctive expansion and disjunctive resolution to clause S5 (the result from the previous reduction) allows deriviation of the minimal clause sub-matrix S11 :
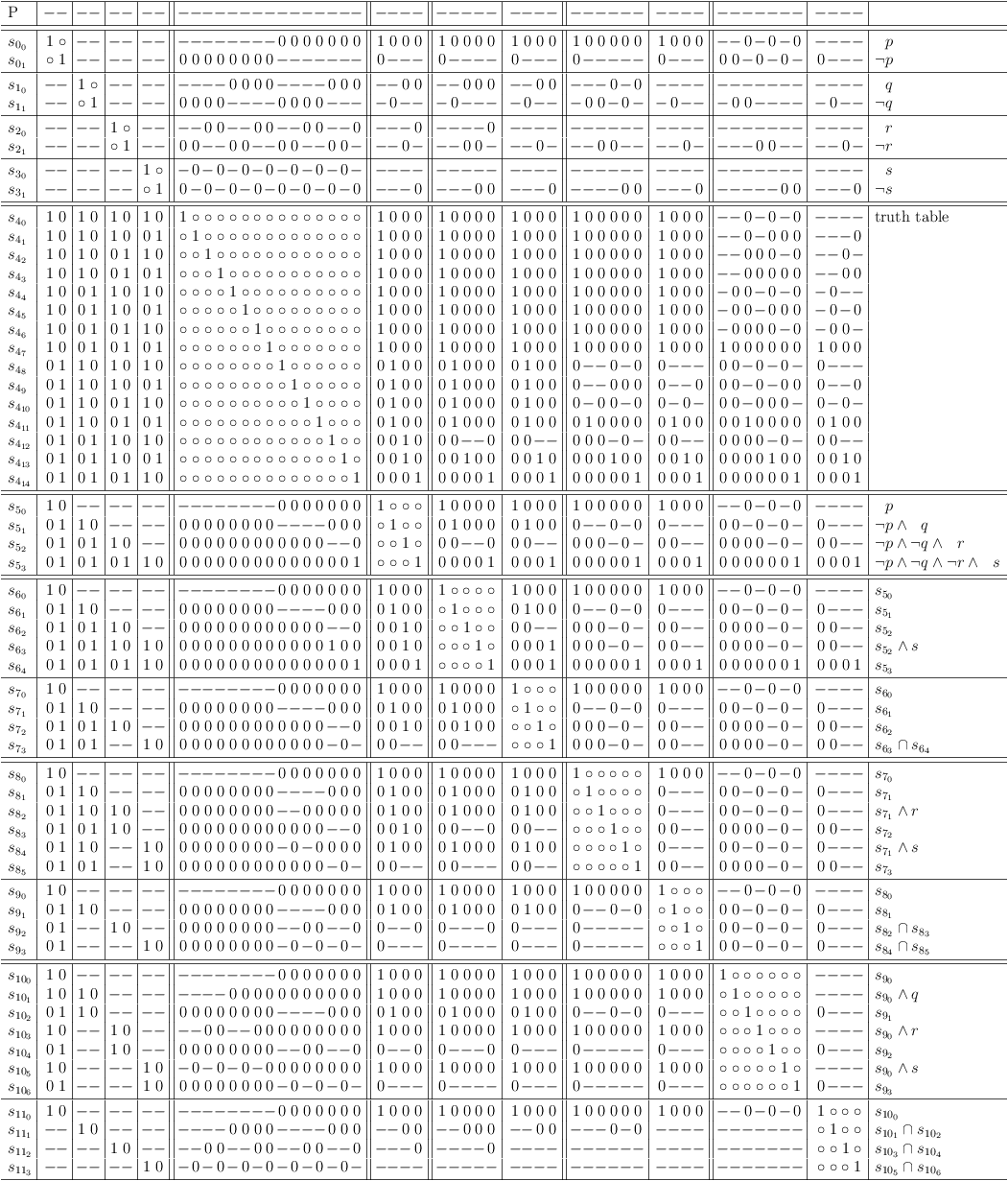
Expansion and resolution for derviation of minimal clause sub-matrix S11 .
Copyright
Copyright (C) 2013, Wolfgang Scherer, <Wolfgang.Scherer@gmx.de>. See the document source for conditions of use under the GNU Free Documentation License.