Indirect Conflicts
| Author: | Wolfgang Scherer |
|---|
Contents
4-SAT Base Problem
Indirect Conflicts are best illustrated in a 4-SAT context.
Boolean formula:
( a0 ∨ a1 ∨ a2 ∨ a3 ) ∧ ( b0 ∨ b1 ∨ b2 ∨ b3 ) ∧ ( c0 ∨ c1 ∨ c2 ∨ c3 ) ∧ ( ¬a0 ∨ ¬c2 ) ∧ ( ¬a0 ∨ ¬c3 ) ∧ ( ¬a1 ∨ ¬c2 ) ∧ ( ¬a1 ∨ ¬c3 ) ∧ ( ¬a2 ∨ ¬c0 ) ∧ ( ¬a2 ∨ ¬c1 ) ∧ ( ¬a3 ∨ ¬c0 ) ∧ ( ¬a3 ∨ ¬c1 ) ∧ ( ¬b0 ∨ ¬c0 ) ∧ ( ¬b0 ∨ ¬c1 ) ∧ ( ¬b1 ∨ ¬c0 ) ∧ ( ¬b1 ∨ ¬c1 ) ∧ ( ¬b2 ∨ ¬c2 ) ∧ ( ¬b2 ∨ ¬c3 ) ∧ ( ¬b3 ∨ ¬c2 ) ∧ ( ¬b3 ∨ ¬c3 )
Clause vectors:
[ 1 1 1 1 _ _ _ _ _ _ _ _ ] [ _ _ _ _ 1 1 1 1 _ _ _ _ ] [ _ _ _ _ _ _ _ _ 1 1 1 1 ] [ 0 _ _ _ _ _ _ _ _ _ 0 _ ] [ 0 _ _ _ _ _ _ _ _ _ _ 0 ] [ _ 0 _ _ _ _ _ _ _ _ 0 _ ] [ _ 0 _ _ _ _ _ _ _ _ _ 0 ] [ _ _ 0 _ _ _ _ _ 0 _ _ _ ] [ _ _ 0 _ _ _ _ _ _ 0 _ _ ] [ _ _ _ 0 _ _ _ _ 0 _ _ _ ] [ _ _ _ 0 _ _ _ _ _ 0 _ _ ] [ _ _ _ _ 0 _ _ _ 0 _ _ _ ] [ _ _ _ _ 0 _ _ _ _ 0 _ _ ] [ _ _ _ _ _ 0 _ _ 0 _ _ _ ] [ _ _ _ _ _ 0 _ _ _ 0 _ _ ] [ _ _ _ _ _ _ 0 _ _ _ 0 _ ] [ _ _ _ _ _ _ 0 _ _ _ _ 0 ] [ _ _ _ _ _ _ _ 0 _ _ 0 _ ] [ _ _ _ _ _ _ _ 0 _ _ _ 0 ] a a a a b b b b c c c c 0 1 2 3 0 1 2 3 0 1 2 3
Satoku Matrix
It can be seen, if e.g. selection rows s00 and s10 are both selected, that clause segments s00, 2, s10, 2 would be filled entirely with zeroes, making s00 and s10 unselectable. Therefore, selecting both s00 and s10 leads to a contradiction.
Plain mapping does not detect the indirect conflicts:
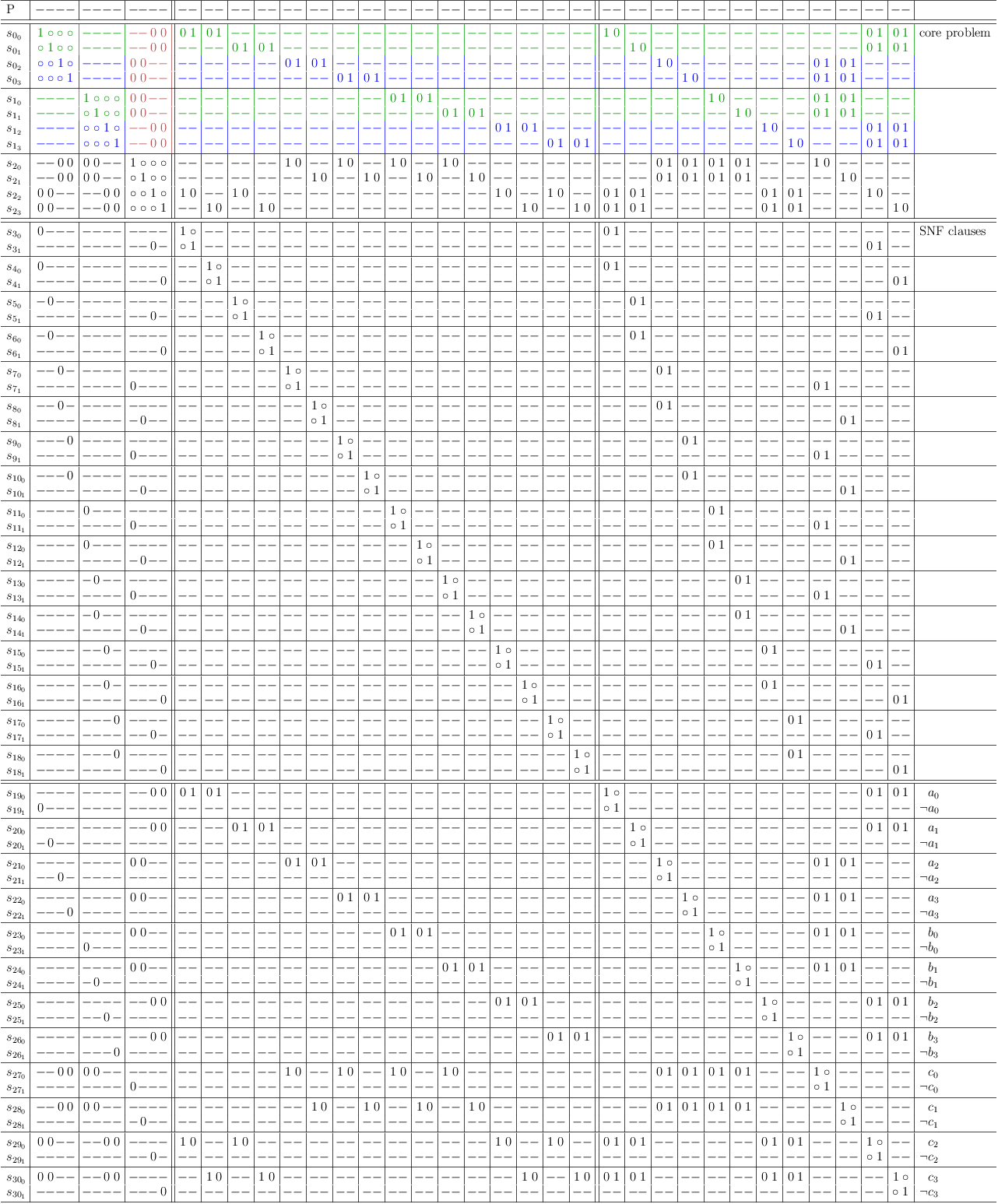
Plain mapping does not detect the indirect conflicts
Conflict maximization does not detect the indirect dependencies:
Conflict maximization does not detect the indirect dependencies
Detecting Indirect Conflicts
It is possible to use combination of selection rows in additional clauses to detect such contradictions.
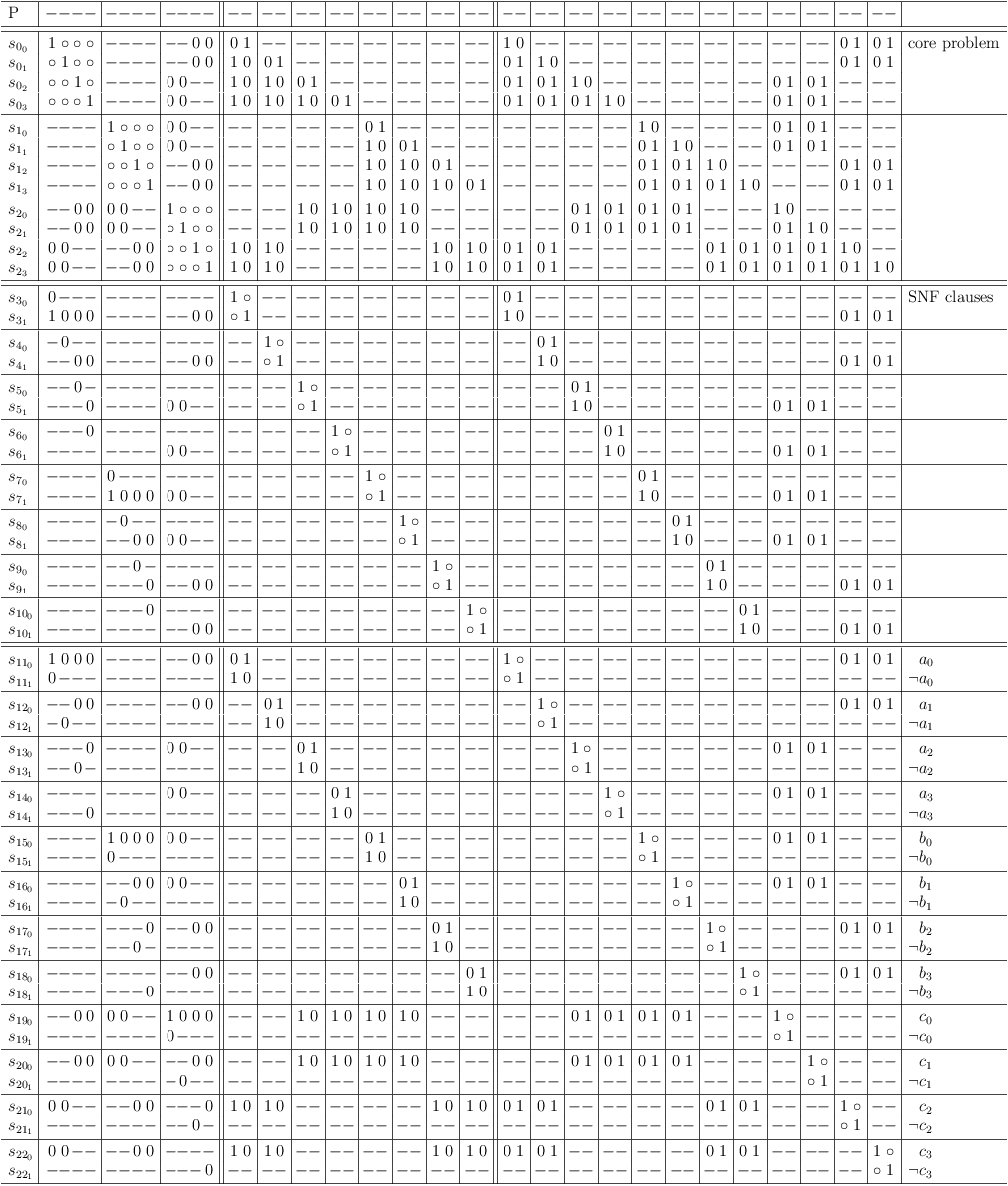
Minimal Combination of 2 Selection Rows
When combining selection rows s00, s10 in a new clause with an alternative that has no dependencies at all:

Combine selection rows s00, s10 minimal
and running the RUA, the conflict is detected. However it is not propagated to the source selection rows:

Combine selection rows s00, s10 minimal, run RUA
Selection Row Variables
Construct variables for selection rows s00, s10

Construct variables for selection rows s00, s10
Combine selection rows s00, s10 via selection row variables
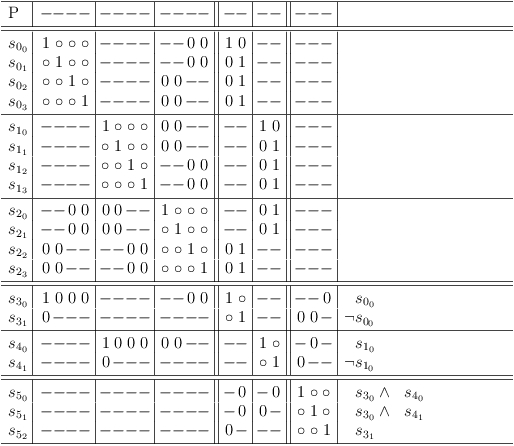
Combine selection rows s00, s10 via selection row variables
Combine selection rows s00, s10 via selection row variables, run RUA
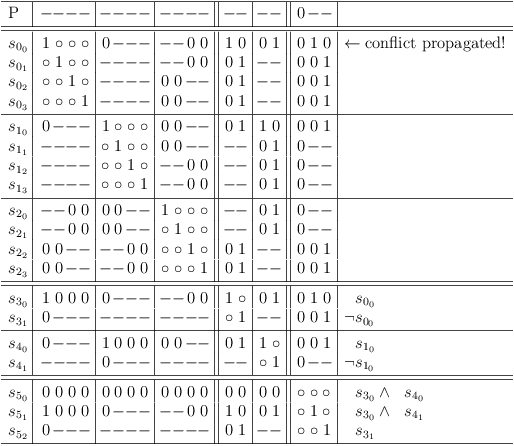
Combine selection rows s00, s10 via selection row variables, run RUA
Combination of 2 Selection Rows with Proper Alternatives
Combine selection rows s00, s11 with alternatives

Combine selection rows s00, s11 with alternatives
Combine selection rows s00, s11 with alternatives, run RUA

Combine selection rows s00, s11 with alternatives, run RUA
Combination of a Selection Row with an Entire Clause Sub-Matrix
Combine selection row s01 with alternative rows s10, s11, s12, s13

Combine selection row s01 with alternative rows s10, s11, s12, s13
Combine selection row s01 with alternative rows s10, s11, s12, s13 , run RUA

Combine selection row s01 with alternative rows s10, s11, s12, s13 , run RUA
Remaining Conflicts
The disambiguation also works with more than one selection row combined with an entire clause sub-matrix.
Full combination of selection rows s02, s03 with sub-matrix S1 , run RUA

Full combination of selection rows s02, s03 with sub-matrix S1 , run RUA
3-SAT Indirect Conflicts
Indirect conflicts in a 3-SAT context are analogous to the 4-SAT context.
Translate 4-SAT to 3-SAT
Translate the 4-SAT problem to a 3-SAT problem by splitting each 4-SAT clause into 2 3-SAT clauses:
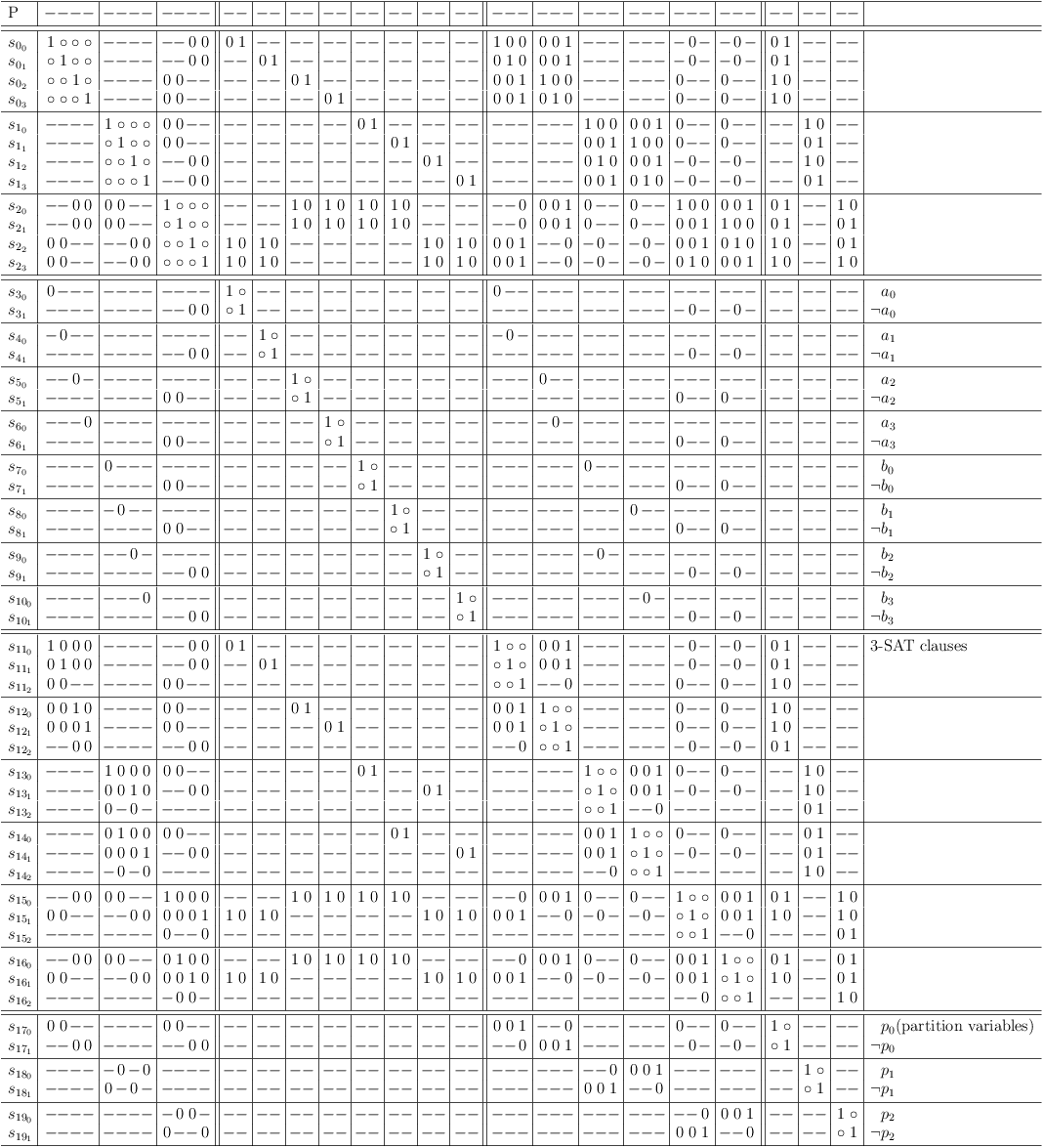
Translate 4-SAT to 3-SAT clauses
Derive boolean problem:
(( ¬a0 ∧ ¬p0 ) ∨ ( ¬a1 ∧ ¬p0 ) ∨ ( p0 )) ∧ (( ¬a2 ∧ p0 ) ∨ ( ¬a3 ∧ p0 ) ∨ ( ¬p0 )) ∧ (( ¬b0 ∧ p1 ) ∨ ( ¬b2 ∧ p1 ) ∨ ( ¬p1 )) ∧ (( ¬b1 ∧ ¬p1 ) ∨ ( ¬b3 ∧ ¬p1 ) ∨ ( p1 )) ∧ (( a2 ∧ a3 ∧ b0 ∧ b1 ∧ ¬p0 ∧ p2 ) ∨ ( a0 ∧ a1 ∧ b2 ∧ b3 ∧ p0 ∧ p2 ) ∨ ( ¬p2 )) ∧ (( a2 ∧ a3 ∧ b0 ∧ b1 ∧ ¬p0 ∧ ¬p2 ) ∨ ( a0 ∧ a1 ∧ b2 ∧ b3 ∧ p0 ∧ ¬p2 ) ∨ ( p2 )
Clause vectors:
[
[ 0 _ _ _ _ _ _ _ 0 _ _ ]
[ _ 0 _ _ _ _ _ _ 0 _ _ ]
[ _ _ _ _ _ _ _ _ 1 _ _ ]
]
[
[ _ _ 0 _ _ _ _ _ 1 _ _ ]
[ _ _ _ 0 _ _ _ _ 1 _ _ ]
[ _ _ _ _ _ _ _ _ 0 _ _ ]
]
[
[ _ _ _ _ 0 _ _ _ _ 1 _ ]
[ _ _ _ _ _ _ 0 _ _ 1 _ ]
[ _ _ _ _ _ _ _ _ _ 0 _ ]
]
[
[ _ _ _ _ _ 0 _ _ _ 0 _ ]
[ _ _ _ _ _ _ _ 0 _ 0 _ ]
[ _ _ _ _ _ _ _ _ _ 1 _ ]
]
[
[ _ _ 1 1 1 1 _ _ 0 _ 1 ]
[ 1 1 _ _ _ _ 1 1 1 _ 1 ]
[ _ _ _ _ _ _ _ _ _ _ 0 ]
]
[
[ _ _ 1 1 1 1 _ _ 0 _ 0 ]
[ 1 1 _ _ _ _ 1 1 1 _ 0 ]
[ _ _ _ _ _ _ _ _ _ _ 1 ]
]
a a a a b b b b p p p
0 1 2 3 0 1 2 3 0 1 2
Remap to satoku matrix:
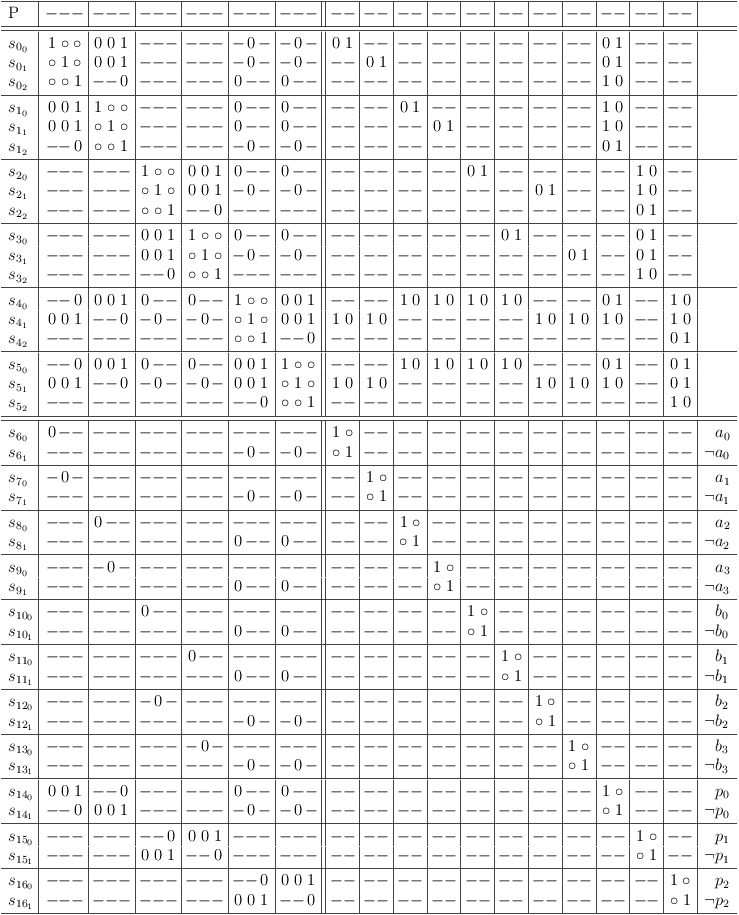
Remapped 3-SAT problem
Detect Indirect Conflicts
Construct variables for selection rows s00, s20
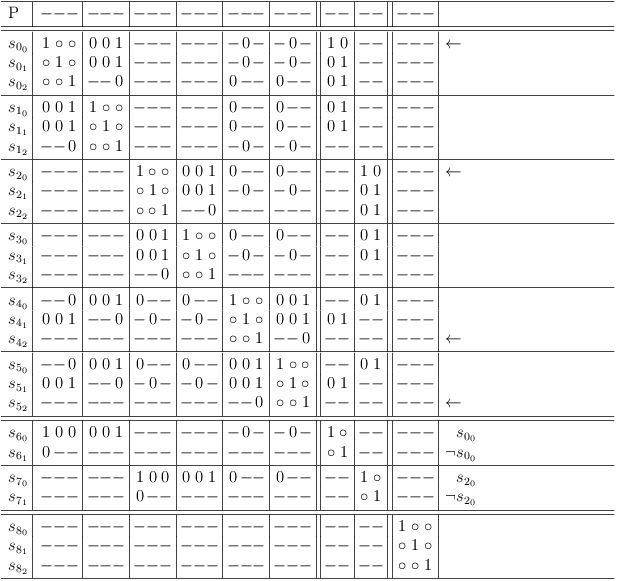
Construct variables for selection rows s00, s20
Combine selection rows s00, s20 via selection row variables

Combine selection rows s00, s20 via selection row variables
Combine selection rows s00, s20 via selection row variables, run RUA
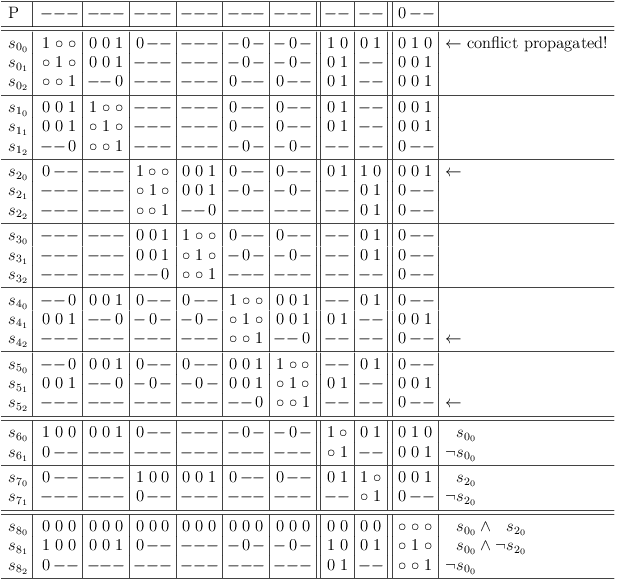
Combine selection rows s00, s20 via selection row variables, run RUA
Indirect 2-SAT Conflicts
In a 2-SAT context, there can only be indirect conflicts, if the requirements update algorithm is not applied.
In this example:
( ¬p ∨ s ) ∧ ( ¬q ∨ s ) ∧ ( p ∨ ¬r ) ∧ ( q ∨ r )
with clause vectors:
[ 0 - - 1 ] [ - 0 - 1 ] [ 1 - 0 - ] [ - 1 1 - ] p q r s
selecting rows s00 and s10 will lead to a contradiction:
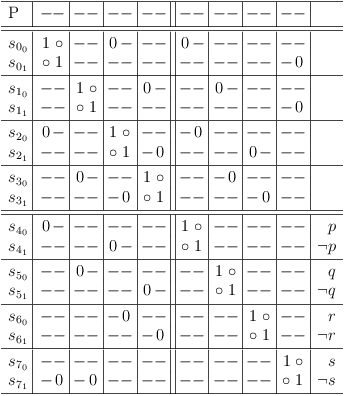
Indirect 2-SAT Conflicts
After running the RUA, all dependencies are detected and propagated.

Indirect 2-SAT Conflicts, run RUA
Since there cannot be any indirect conflicts, unsatisfiability of a 2-SAT problem is detected after the initial RUA run.
If it was possible for 2-SAT problems to have indirect conflicts, it would also be possible to translate any k-SAT problem for k ≥ 3 to a 2-SAT problem.
1-SAT Conflicts
Trivially, 1-SAT conflicts signify unsatisfiablity. Therefore there cannot be any conflicts at all, if a 1-SAT problem is satisfiable.
Boolean formula:
( p ) ∧ ( ¬q ) ∧ ( ¬r ) ∧ ( s )
Clause vectors:
[ 1 _ _ _ ] [ _ 0 _ _ ] [ _ _ 0 _ ] [ _ _ _ 1 ] p q r s
Satoku matrix:
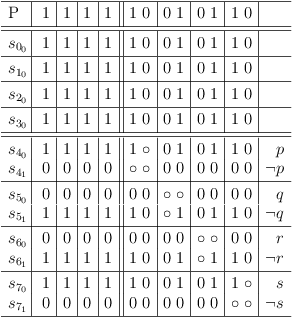
1-SAT conflicts signify unsatisfiablity
Copyright
Copyright (C) 2013, Wolfgang Scherer, <Wolfgang.Scherer@gmx.de>. See the document source for conditions of use under the GNU Free Documentation License.