2-SAT Solutions
| Author: | Wolfgang Scherer |
|---|
Contents
Base Problem
Boolean Formula:
( ¬a0 ∨ ¬a1 ) ∧ ( ¬a2 ∨ ¬a3 ) ∧ ( ¬a4 ∨ ¬a5 ) ∧ ( ¬a6 ∨ ¬a7 ) ∧ ( ¬a8 ∨ ¬a9 ) ∧ ( ¬b0 ∨ ¬b1 )
Clause Vectors:
[ 0 0 _ _ _ _ _ _ _ _ _ _ ] [ _ _ 0 0 _ _ _ _ _ _ _ _ ] [ _ _ _ _ 0 0 _ _ _ _ _ _ ] [ _ _ _ _ _ _ 0 0 _ _ _ _ ] [ _ _ _ _ _ _ _ _ 0 0 _ _ ] [ _ _ _ _ _ _ _ _ _ _ 0 0 ] a a b b c c d d e e f f 0 1 0 1 0 1 0 1 0 1 0 1
Satoku Matrix Without Conflict Maximization

000-check-2-sat-solutions.r.v-000.png
Colored matrix:
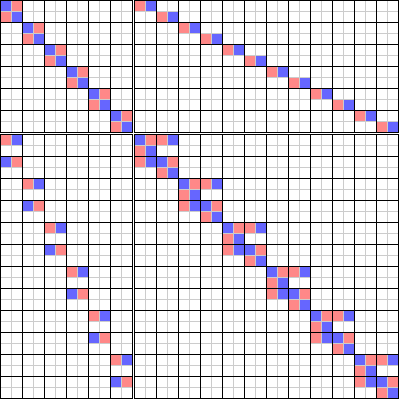
000-check-2-sat-solutions.r.v-000.cm.png
Solution Set
The solution set delivers all optimal solutions. However, they are not unique.
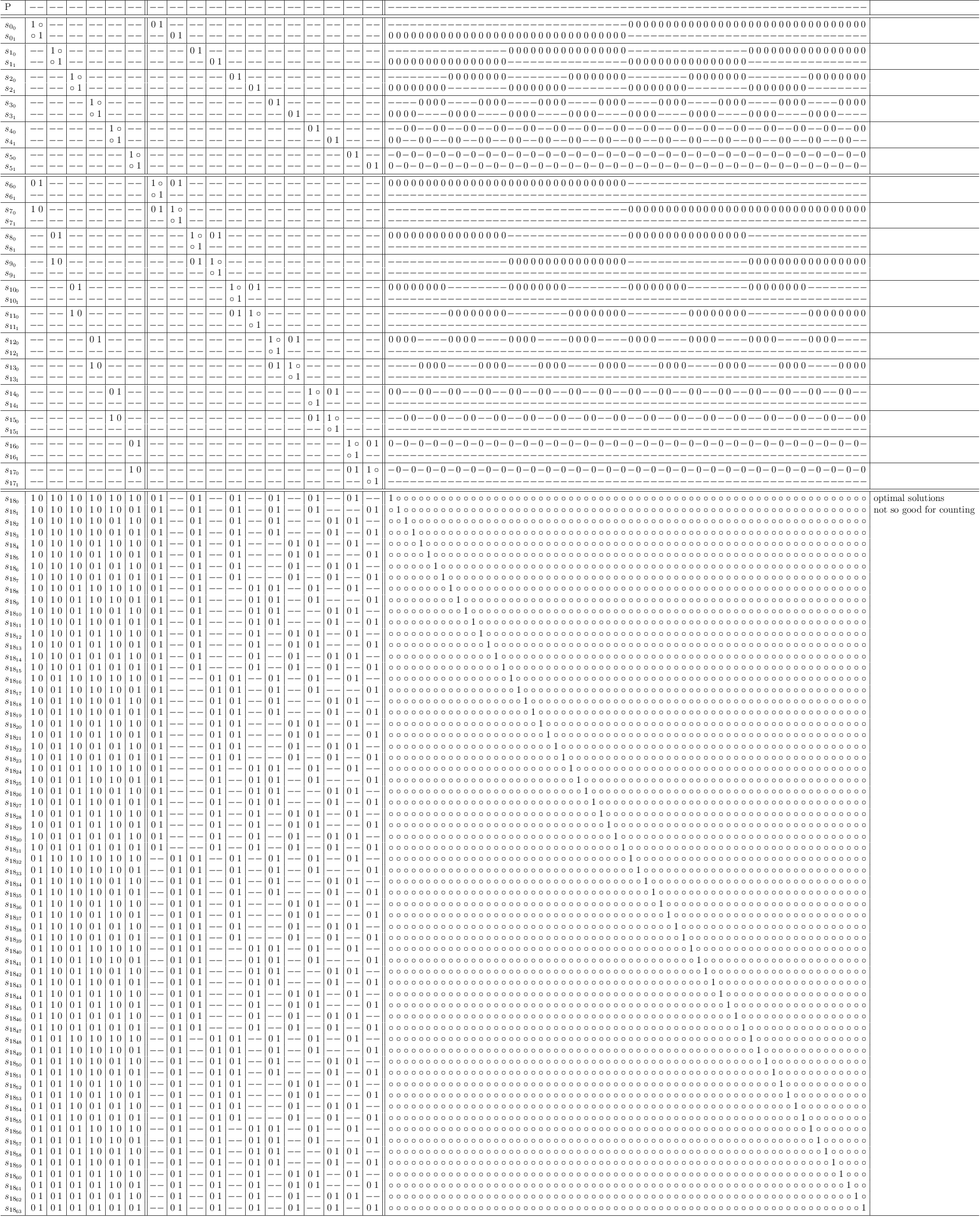
000-check-2-sat-solutions.r.v-001.png
Colored matrix:
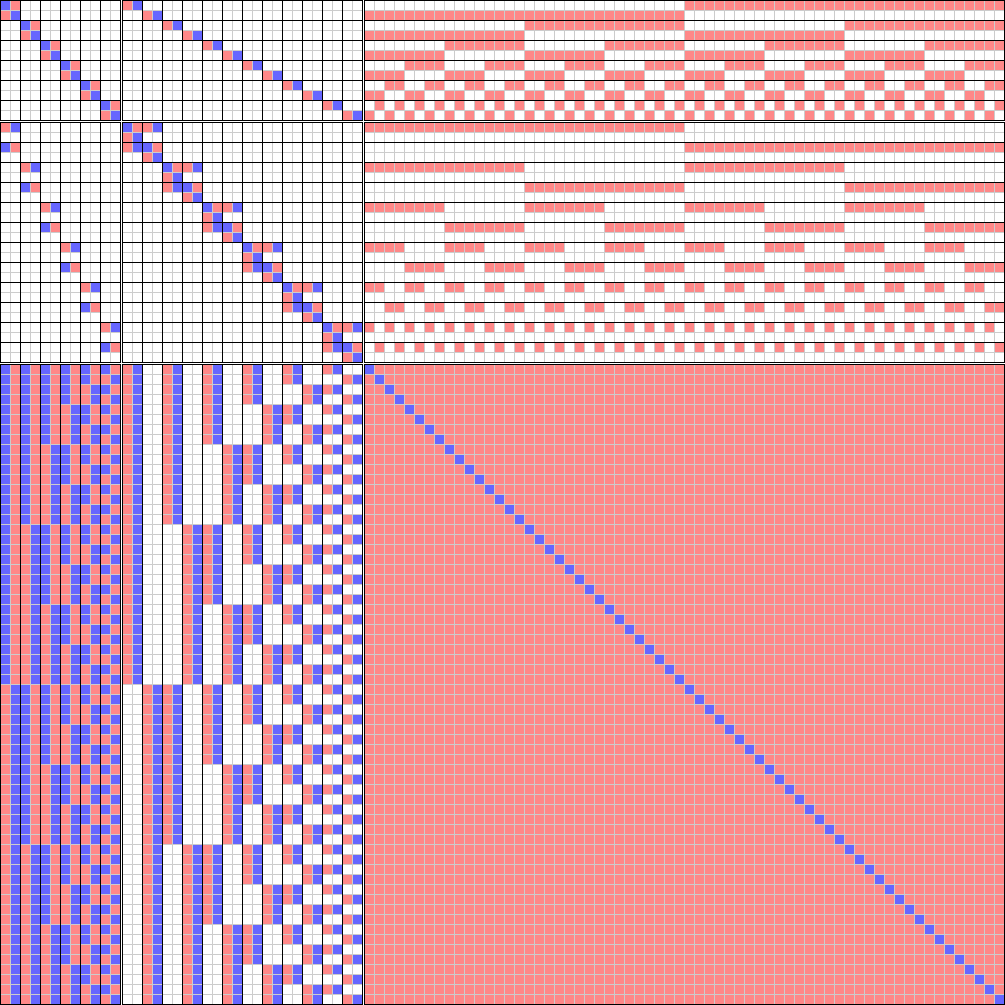
000-check-2-sat-solutions.r.v-001.cm.png
Satoku Matrix With Conflict maximization

000-check-2-sat-solutions.c.v-000.png
Color matrix:
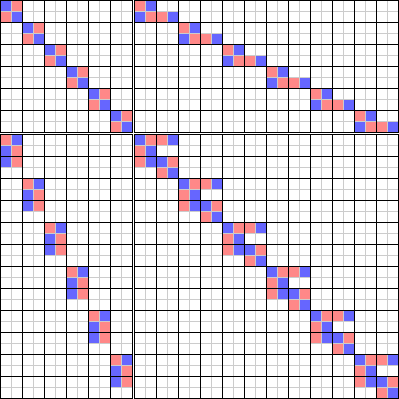
000-check-2-sat-solutions.c.v-000.cm.png
Solution Set
The solution set delivers unique solutions. However, they are not all optimal.

000-check-2-sat-solutions.c.v-001.png
Color matrix:
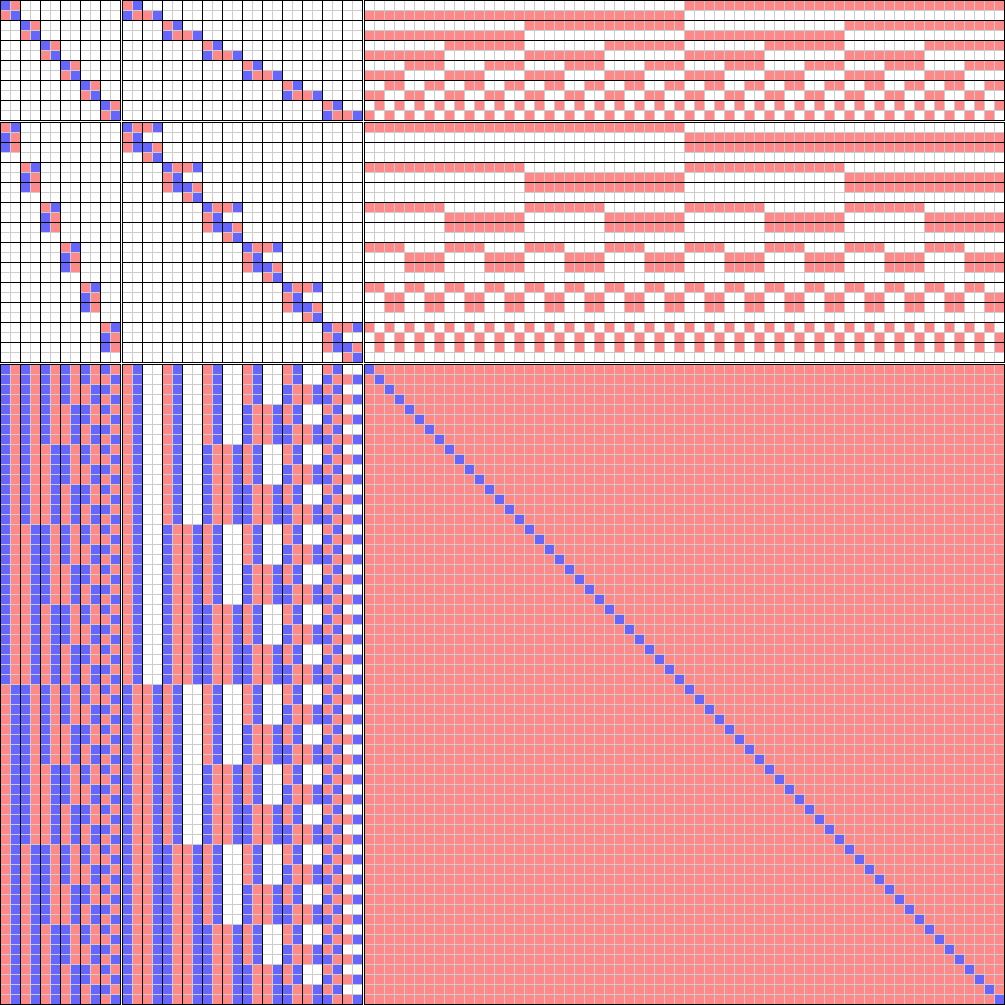
000-check-2-sat-solutions.c.v-001.cm.png
Count Solutions
| 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 2^6 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 2^5 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 2^5 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 2^4 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 2^5 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 2^4 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 2^4 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 2^3 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 2^5 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 2^4 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 2^4 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 2^3 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 2^4 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 2^3 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 2^3 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 2^2 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 2^5 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 2^4 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 2^4 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 2^3 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 2^4 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 2^3 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 2^3 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 2^2 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 2^4 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 2^3 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 2^3 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 2^2 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 2^3 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 2^2 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 2^2 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 2^1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 2^5 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 2^4 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 2^4 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 2^3 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 2^4 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 2^3 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 2^3 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 2^2 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 2^4 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 2^3 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 2^3 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 2^2 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 2^3 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 2^2 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 2^2 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 2^1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 2^4 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 2^3 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 2^3 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 2^2 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 2^3 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 2^2 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 2^2 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 2^1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 0 1 | _ _ | 2^3 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 1 0 | 0 1 | 2^2 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 0 1 | _ _ | 2^2 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 1 0 | 0 1 | 2^1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 0 1 | _ _ | 2^2 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 1 0 | 0 1 | 2^1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 0 1 | _ _ | 2^1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 0 | 0 1 | 2^0
_ _ | _ _ | _ _ | _ _ | _ _ | _ _ | 6 _ _ | _ _ | _ _ | _ _ | _ _ | 5 _ _ | _ _ | _ _ | _ _ | _ _ | 5 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | _ _ | _ _ | 5 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | 3 _ _ | _ _ | _ _ | _ _ | _ _ | 5 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | 3 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | 3 _ _ | _ _ | _ _ | 3 _ _ | _ _ | 2 _ _ | _ _ | _ _ | _ _ | _ _ | 5 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | 3 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | 3 _ _ | _ _ | _ _ | 3 _ _ | _ _ | 2 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | 3 _ _ | _ _ | _ _ | 3 _ _ | _ _ | 2 _ _ | _ _ | _ _ | 3 _ _ | _ _ | 2 _ _ | _ _ | 2 _ _ | 1 _ _ | _ _ | _ _ | _ _ | _ _ | 5 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | 3 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | 3 _ _ | _ _ | _ _ | 3 _ _ | _ _ | 2 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | 3 _ _ | _ _ | _ _ | 3 _ _ | _ _ | 2 _ _ | _ _ | _ _ | 3 _ _ | _ _ | 2 _ _ | _ _ | 2 _ _ | 1 _ _ | _ _ | _ _ | _ _ | 4 _ _ | _ _ | _ _ | 3 _ _ | _ _ | _ _ | 3 _ _ | _ _ | 2 _ _ | _ _ | _ _ | 3 _ _ | _ _ | 2 _ _ | _ _ | 2 _ _ | 1 _ _ | _ _ | _ _ | 3 _ _ | _ _ | 2 _ _ | _ _ | 2 _ _ | 1 _ _ | _ _ | 2 _ _ | 1 _ _ | 1 | 0
2^6 + 2^5 + 2^5 + 2^4 + 2^5 + 2^4 + 2^4 + 2^3 + 2^5 + 2^4 + 2^4 + 2^3 + 2^4 + 2^3 + 2^3 + 2^2 + 2^5 + 2^4 + 2^4 + 2^3 + 2^4 + 2^3 + 2^3 + 2^2 + 2^4 + 2^3 + 2^3 + 2^2 + 2^3 + 2^2 + 2^2 + 2^1 + 2^5 + 2^4 + 2^4 + 2^3 + 2^4 + 2^3 + 2^3 + 2^2 + 2^4 + 2^3 + 2^3 + 2^2 + 2^3 + 2^2 + 2^2 + 2^1 + 2^4 + 2^3 + 2^3 + 2^2 + 2^3 + 2^2 + 2^2 + 2^1 + 2^3 + 2^2 + 2^2 + 2^1 + 2^2 + 2^1 + 2^1 + 2^0 = 729
Copyright
Copyright (C) 2013, Wolfgang Scherer, <Wolfgang.Scherer@gmx.de>. See the document source for conditions of use under the GNU Free Documentation License.